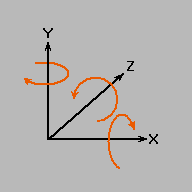
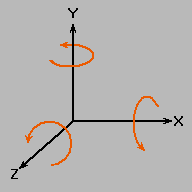
Why are they even called right-handed or left-handed? Basically, it's a simple trick to remember orientations. Hold your hand flat, with your thumb perpendicular to your fingers. Now imagine that your thumb is the axis of rotation and wrap your fingers to your palm. If you used your left hand, your fingers wrapped clockwise around your thumb. If you used your right hand, your fingers wrapped counter-clockwise. This will help you remember which way something rotates about an axis in right- or left-handed coordinates.
Also, the direction of the cross product of two vectors can be visualized thus: Suppose you want to find the direction of A cross B. Put your little finger on vector A, and wrap your fingers toward B, sweeping across the acute (small) angle. Your thumb will point in the direction of the resultant cross product vector. This direction again depends on which hand you use.
Using this, note that Z = X cross Y, X = Y cross Z, and Y = Z cross X. If X points to the right, Y points up, and you're using right-handed coordinates, Z will poke you in the eye. If you're using left-handed coordinates, Z points into the screen.
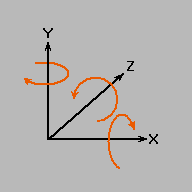 |
Note, by the way, that if X points to the right and Y up (as in these illustrations), rotations about the Z axis appear counter-clockwise to you, regardless of whether you're using left or right handed coordinates. | 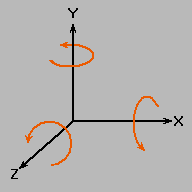 |
| Left-Handed Coordinates | Right-Handed Coordinates |